바나흐 고정점 정리(Banach Fixed-point Theorem)와 고정점 반복(Fixed-point Iteration)

이 글에서는 바나흐 고정점 정리(Banach Fixed-point Theorem)와 고정점 반복(Fixed-point Iteration)에 대해 설명할 것이다.

개요

어떤 함수 $f$의 고정점(fixed point)은 $f(x) = x$를 만족하는 $x$를 의미한다. $f$를 어떤 변환으로 간주했을 때, 고정점은 변환 $f$에 의해 변하지 않는(고정된) 값이라고 할 수 있다. 예를 들어 $f(x) = 2x - 1$의 고정점은 $1$이다. 고정점은 함수에 따라 여러 개 존재할 수도 있고, 존재하지 않을 수도 있다. 예를 들어 $f(x) = x^2$의 고정점은 $0, 1$로 총 2개이고, $f(x) = x+1$은 고정점을 가지지 않는다.

바나흐 고정점 정리(Banach fixed-point theorem) 또는 축소사상정리(contraction mapping theorem)는 함수가 유일한 고정점을 가질 충분조건을 제시한다. 정리는 다음과 같다.

$(X, d)$가 완비 거리 공간(complete metric space)이고 함수 $f : X \rightarrow X$가 축소사상(contraction mapping)일 때, $f$는 유일한 고정점을 가진다.

완비 거리 공간은 임의의 코시 수열이 항상 극한을 가지는 거리 공간이다. 가장 대표적인 예가 실수 집합이다. 이 개념이 익숙하지 않다면 실수 집합이나 닫힌 구간으로 생각해도 좋다.

축소사상은 어떤 $0 \le k < 1$에 대해 다음을 만족하는 함수이다. 임의의 두 점 간의 거리를 $k < 1$배 이하로 축소시키는 변환이라고 할 수 있다.

\[d(f(x), f(y)) \le k d(x, y)\]

추가로, 정리의 증명 과정에서 수열 $a_{n+1} = f(a_n)$는 초항과는 무관하게 항상 $f$의 고정점으로 수렴함을 알 수 있다. 따라서 충분히 큰 $n$에 대한 $a_n$ 값을 계산함으로써 $f$의 고정점의 근삿값을 충분히 작은 오차로 구할 수 있다. 이 과정을 고정점 반복(fixed-point iteration)이라고 한다.

바나흐 고정점 정리는 상당히 직관적인 정리이다. 어떤 변환이 공간의 모든 점들 간의 거리를 일정 비율 이하로 축소시킨다면, 이 변환을 무한 번 반복하면 결국 모든 점들이 한 점으로 모이게 될 것이다.

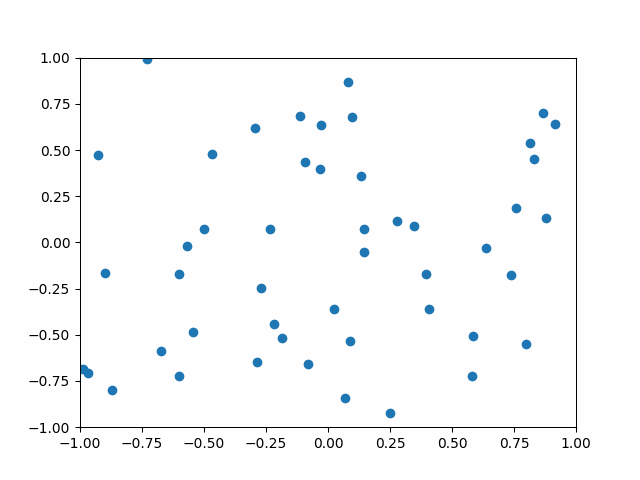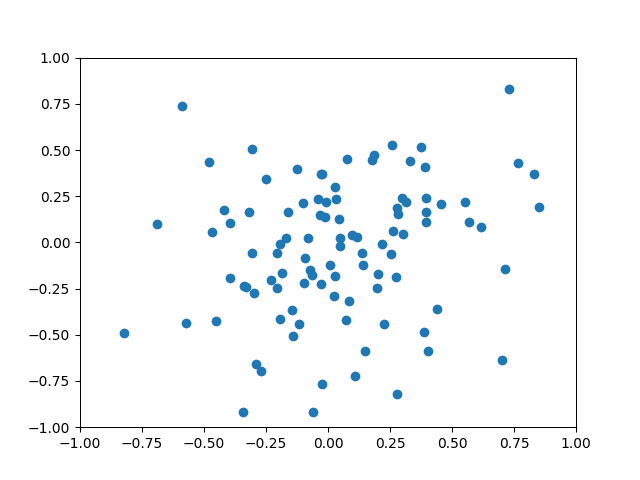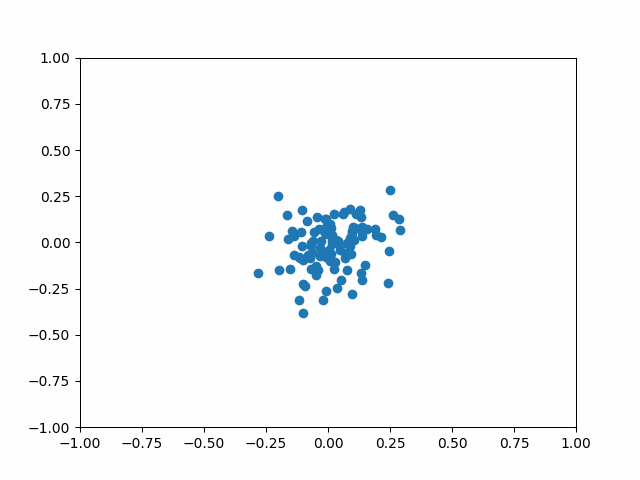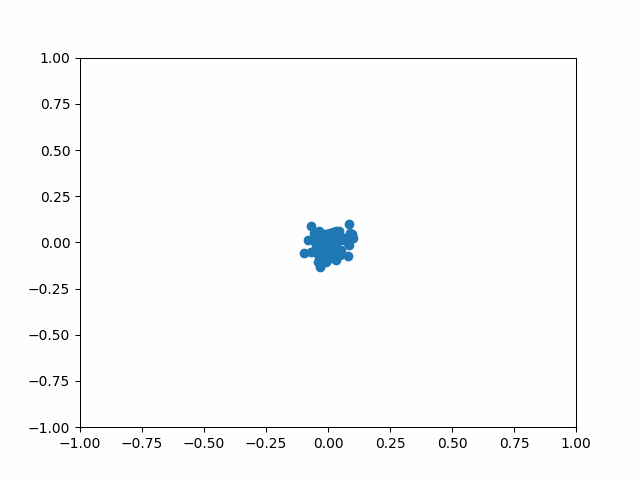
축소사상 여부 확인 방법

어떤 함수가 축소사상인지를 확인하기 위한 가장 기본적인 방법은 정의의 부등식을 만족하는지 직접 확인하는 것이다. 예를 들어 $[1, \infty)$에 정의된 $f(x) = \sqrt x$의 경우

\[\left\lvert \sqrt x - \sqrt y \right\rvert = \left\lvert \frac{x - y}{\sqrt x + \sqrt y} \right\rvert \le \frac{1}{2} \left\lvert x - y \right\rvert\]

이므로 축소사상임을 알 수 있다. 그러나 일반적으로 이를 보이는 과정은 쉽지 않다.

함수가 미분가능한 경우 도함수의 값을 사용하여 축소사상 여부를 확인할 수 있다. 만약 특정 구간에서 $f$가 미분가능하며 도함수의 절댓값이 $k < 1$ 이하일 경우, $f$는 해당 구간에서 축소사상이다. 그 이유는 평균값 정리로부터 쉽게 알 수 있다. 평균값 정리에 의해 구간 내 두 점 $x$, $y$에 대해

\[f(x) - f(y) = f'(z) (x - y)\]

가 성립한다. 여기서 $z$는 $x$, $y$ 사이의 어떤 점이다. 이 식에 절댓값을 씌우면

\[\left\lvert f(x) - f(y) \right\rvert = \left\lvert f'(z) \right\rvert \left\lvert x - y \right\rvert \le k \left\lvert x - y \right\rvert\]

이다. 따라서 $f$는 축소사상이다.

예제

예제 1

(문제) 방정식 $e^x - 3x = 0$의 해 중 구간 $[0, 1]$ 내에 존재하는 것은 단 하나임 보여라.

(풀이) $f : [0, 1] \rightarrow [0, 1]$가 $f(x) = e^x / 3$라고 하자. 주어진 방정식은 $f(x) = x$로 쓸 수 있으므로 방정식의 해는 $f$의 고정점과 같다. $f$의 도함수는 $f’(x) = e^x / 3$이다. $f’(x)$의 최솟값은 $f’(0) = 0$, 최댓값은 $f’(1) = e / 3 < 1$이다. 도함수의 절댓값의 상한이 $e / 3 < 1$이므로 $f$는 축소사상이다. 따라서 바나흐 고정점 정리에 의해 $f$는 단 하나의 고정점을 가진다.

예제 2

(문제) 다음과 같이 정의되는 수열 $\{ a_n \}$이 수렴함을 증명하고 수렴값을 구하라.

\[a_1 = 0, \quad a_{n+1} = \left( 2{a_n}^2 + 9 \right)^\frac{1}{3}\]

(풀이) $f(x) = \left( 2x^2 + 9 \right)^\frac{1}{3}$이라고 하자. 그러면 $a_{n+1} = f(a_n)$이다. $f(x)$는 실수 전체에서 두 번 미분 가능하며, 일계도함수와 이계도함수는 다음과 같다.

\[f'(x) = \frac{4x}{3 (2x^2 + 9)^\frac{2}{3} } \\ f'' (x) = - \frac{4(2x^2 - 27)}{9(2x^2 + 9)^\frac{5}{3}}\]

$x$가 양의 무한대와 음의 무한대로 갈 때 $f’(x)$의 극한은 다음과 같다 (로피탈의 정리 사용).

\[\lim_{x \rightarrow \infty} f'(x) = \lim_{x \rightarrow \infty} \frac{4x}{3 (2x^2 + 9)^\frac{2}{3} } = \lim_{x \rightarrow \infty} \frac{4}{8x {(2x^2 + 9)}^{-\frac{1}{3}} } = 0\\ \lim_{x \rightarrow -\infty} f'(x) = \lim_{x \rightarrow -\infty} \frac{4x}{3 (2x^2 + 9)^\frac{2}{3} } = \lim_{x \rightarrow -\infty} \frac{4}{8x {(2x^2 + 9)}^{-\frac{1}{3}} } = 0\\\]

따라서 $f’(x)$는 극점에서 최댓값과 최솟값을 갖는다.

$f’’ (x) = 0$인 $x$는 $\pm 3\sqrt{\frac{3}{2}}$이다. 이때 $f’(x)$의 값은 각각 $\sqrt[6]{6}/3 , -\sqrt[6]{6}/3$이다. 따라서 두 값이 각각 $f’(x)$의 최댓값과 최솟값이다. 따라서 $\lvert f’(x) \rvert \le \sqrt[6]{6}/3 < 1$이다. 따라서 $f$는 축소사상이며, 바나흐 고정점 정리에 의해 $\{ a_n \}$은 $f$의 고정점으로 수렴한다.

$f$의 고정점은 $x = {(2x^2 + 9)}^{\frac{1}{3}}$를 만족하는 $x = 3$이다. 따라서 $\{ a_n \}$은 $3$으로 수렴한다.

예제 3

(문제) 다음과 같이 정의되는 수열 $\{ a_n \}$이 수렴함을 증명하고 수렴값을 구하라.

\[a_1 = 1, \quad a_{n+1} = 1 + a_n - \frac{1}{2} {a_n}^2\]

(풀이) $f(x) = 1 + x - \frac{1}{2} x^2$이라고 하자. 그러면 $a_{n+1} = f(a_n)$이다. $f$의 도함수는 $f’(x) = 1 - x$이다. 도함수의 절댓값을 살펴봄으로써, $f$는 $(0, 2)$ 구간 내의 임의의 닫힌 구간에서 축소사상이며, $(-\infty, 0]\cup[2, \infty)$에서는 축소사상이 아님을 알 수 있다. 따라서 바나흐 고정점 정리를 사용하기 위해서는 $f$가 정의역 전체에서 축소사상이 되도록 정의해야 한다.

$f$는 국소적으로는 축소사상이므로, $f$의 정의역을 제한함으로써 전 영역에서 축소사상인 함수로 만들 수 있다. 또한 고정점 정리를 사용하기 위해서는 $f$의 공역이 정의역과 같아야 한다. $f$의 정의역과 공역을 $[1, 3/2]$로 제한하자. 모든 $x \in [1, 3/2]$에 대해 $f(x) \in [1, 3/2]$이므로 모든 함숫값은 공역에 포함되어 잘 정의된다. $f$의 도함수의 절댓값은 $[1, 3/2]$에서 $1/2$ 이하이므로 $f$는 축소사상이다. 따라서 바나흐 고정점 정리에 의해 $\{ a_n \}$은 $f$의 고정점 $\sqrt{2}$로 수렴한다.

증명

먼저 고정점의 존재성을 증명할 것이다. 수열 $\{ x_n \}$을 다음과 같이 정의하자.

\[x_0 \in X, \quad x_{n+1} = f(x_n)\]

$x_0$은 정의역 상의 임의의 점이다. $\{ x_n \}$이 $f$의 고정점으로 수렴함을 보임으로써 고정점이 존재한다는 것을 증명할 것이다.

임의의 $n$에 대해 $d(f(x_{n+1}) - f(x_n)) \le k d(x_{n+1}, x_n)$이 성립한다. 따라서

\[d(x_{n+1}, x_n) = d(f(x_n), f(x_{n-1})) \\ \le k d(x_{n}, x_{n-1}) = k d(f(x_{n-1}, x_{n-2})) \\ \cdots \\ \le k^n d(x_1, x_0)\]

에 의해 $d(x_{n+1} - x_n) \le k^n d(x_1, x_0)$이다.

이제 $\{ x_n \}$가 코시 수열임을 보이자. $m, n$은 $m > n$을 만족하는 임의의 자연수라고 하자. 그러면 다음이 성립한다.

\[d(x_m, x_n) \le \left( d(x_m, x_{m-1}) + \ldots + d(x_{n+1} - x_n) \right) \\ \le \left( k^{m-1} d(x_1, x_0) + \ldots + k^n d(x_1 - x_0) \right) \\ = (k^{m-1} + \ldots + k^n) d(x_1 - x_0) \\ = k^n (k^{m-n-1} + \ldots + k^0) d(x_1 - x_0) \\ \le k^n \sum_{i=0}^{\infty} k^i d(x_1 - x_0) = \frac{k^n}{1-k} d(x_1 - x_0)\]

위 식에서 첫 번째 줄은 삼각부등식에 의한 것이다. 두 번째 줄은 앞에서 구한 각 $d(x_{i+1}, x_i)$에 대한 부등식을 적용한 것이다.

$n$이 무한대로 커진다면 $0 \le k < 1$이므로 $k^n / (1 - k) d(x_1 - x_0)$의 값은 $0$으로 수렴한다. 따라서 $d(x_m, x_n)$ 역시 $0$으로 수렴한다. 따라서 $\{ x_n \}$는 코시 수열이다.

거리공간 $X$가 완비이므로 코시 수열인 $\{ x_n \}$는 어떤 점 $x$로 수렴한다. 이제 이것이 $f$의 고정점임을 보이자.

$f$는 축소사상이므로 립시츠 연속이다. 따라서 연속함수이다. 연속함수의 성질에 의해 다음이 성립한다.

\[\lim_{n \rightarrow \infty} f(x_n) = f(\lim_{n \rightarrow \infty} x_n) = f(x)\]

또한

\[x = \lim_{n \rightarrow \infty} x_{n+1} = \lim_{n \rightarrow \infty} f(x_n)\]

이 성립한다. 두 식으로부터 $x = f(x)$임을 알 수 있다. 따라서 $\{ x_n \}$의 극한값 $x$는 $f$의 고정점이다. 따라서 $f$의 고정점은 적어도 하나 이상 존재한다.

지금까지 고정점의 존재성을 보였다. 이제 고정점이 존재한다면 유일하다는 것을 증명할 것이다. 증명은 매우 간단하다.

두 점 $x, y$가 $f$의 고정점이라고 하자. 그러면 다음이 성립한다.

\[d(x, y) = d(f(x), f(y)) \le k d(x, y)\]

$0 \le k < 1$이므로 위 부등식이 성립하려면 $d(x, y) = 0$이어야 한다. 거리공간의 정의에 따라 $x = y$이다. 따라서 서로 다른 두 개의 고정점은 존재할 수 없다. 따라서 고정점은 유일하다.

존재성의 증명 과정에서는 정리의 전제조건이 모두 사용되었다. 반면 유일성을 증명하는 데는 $f$가 축소사상이라는 조건 외에는 필요한 것이 없다. 즉 $f$가 축소사상이라면 $X$가 완비가 아니거나 $f$의 정의역과 공역이 일치하지 않는 경우에도 유일성이 성립한다.

적용되지 않는 예

당연하지만 정리를 사용하기 위해서는 필요한 조건을 모두 만족해야 한다. 여기서는 바나흐 고정점 정리에서 간과하기 쉬운 일부 조건이 누락되었을 때 생기는 반례를 보여줄 것이다.

정의역과 공역의 불일치

함수의 정의역과 공역이 일치하지 않는 경우 고정점 반복이 잘 정의되지 않으므로 바나흐 고정점 정리를 적용할 수 없다. 예를 들어, $f : [0, 1] \rightarrow [1, 2]$이 모든 $x$에 대해 $f(x) = \frac{1}{2} x + 1$이라고 하자. 그러면 $f$는 정의역 전체에서 축소사상이지만 고정점은 존재하지 않는다. 만약 $x = 1$에서 고정점 반복을 시작한다면 다음 수는 $f(1) = 3/2$가 되어 $f$의 정의역을 벗어난다. 따라서 고정점 반복이 잘 정의되지 않고, 바나흐 고정점 정리도 적용되지 않는다. $f$의 정의역을 $[0, 1]$로 설정하면 $f$의 치역은 $[1, 3/2]$가 되므로 치역을 포함해야 하는 공역은 정의역과 같은 $[0, 1]$이 절대 될 수 없다. 따라서 바나흐 고정점 정리를 적용하려면 정의역을 잘 설정해야 한다.

완비가 아닌 거리공간

바나흐 고정점 정리의 증명은 우선 고정점 반복의 수열이 코시 수열임을 보이고, 완비성에 의해 극한이 존재함을 보임으로써 고정점의 존재성을 밝힌다. 따라서 거리공간이 완비가 아닌 경우 이런 논증이 더 이상 옳지 않게 된다.

예제 3에서 구간 $f$가 정의된 거리공간을 실수 구간 $[1, 3/2]$ 대신 유리수 구간 $[1, 3/2]\cap \mathbb{Q}$으로 바꾸자. 이제 거리공간은 더 이상 완비가 아니다. $f(x)$의 고정점은 $x = 1 + x - x^2/2$를 만족하는 $x$이다. 즉 $x^2 = 2$를 만족하는 $x$이다. 그러나 (방정식의 해인 $\pm \sqrt 2$가 무리수이므로) 이러한 유리수 $x$는 존재하지 않는다. 따라서 $f$의 고정점은 존재하지 않는다.

축소사상 조건 약화

함수 $f(x)$가 다음 조건을 만족한다고 하자.

\[d(f(x), f(y)) < d(x, y)\]

언뜻 보면 축소사상과 같은 것 같지만 그렇지 않다. 위 조건은 축소사상의 조건보다 약화된 것으로, 축소사상은 위 조건을 항상 만족하지만 역은 성립하지 않는다. 위 조건을 만족하지만 축소사상이 아닌 경우 바나흐 고정점 정리를 적용할 수 없다.

간단한 반례로 다음이 있다. $f : [0, \infty) \rightarrow [0, \infty)$가 $f(x) = \sqrt{x^2 + 1}$라고 하자. 그러면

\[\lvert f'(x) \rvert = \frac{\lvert x \rvert}{\sqrt{x^2 + 1}} < 1\]

이므로 $f(x)$는 위 조건을 만족한다. 그러나 $x$가 무한대로 가면 도함수가 $1$로 수렴하므로 $f$는 축소사상이 아니다. 따라서 바나흐 고정점 정리를 적용할 수 없다. 실제로 $f$는 고정점을 가지지 않는다.

응용

바나흐 고정점 정리는 많은 곳에서 활용되는 중요한 정리이다. 축소사상이라는 조건은 까다롭지만, 일단 만족한다면 바로 고정점의 존재성, 유일성과 계산 알고리즘(고정점 반복)까지 얻을 수 있다는 점에서 강력하다. 또한 바나흐 고정점 정리의 거리공간은 완비성만 만족하면 무엇이든 가능하다. 따라서 함수들로 이루어진 완비거리공간 등에 적용하는 것이 가능하다.

우선 가장 간단한 활용 방법 중 하나는 위의 예제에서 본 것과 같이 수열의 수렴성을 확인하는 것이다.

더욱 심층적인 분야에서의 대표적인 활용 예로는 피카르-린델뢰프 정리(Picard–Lindelöf theorem)가 있다. 이 정리는 초기 조건이 주어진 일계 상미분방정식의 해의 존재성과 유일성을 보장하는 중요한 정리이다. 정리의 증명에서는 함수로 구성된 완비거리공간과 고정점이 미분방정식의 해가 되는 (함수를 입력으로 받는) 함수를 정의한다. 그 다음 이 함수가 축소사상임을 증명한 후 바나흐 고정점 정리를 적용하여 미분방정식의 해(고정점)이 유일하게 존재함을 보인다.

고정점 반복의 경우 충분히 많은 시행을 하면 함수의 고정점을 근사할 수 있다는 점을 활용하여 방정식의 해를 수치적으로 구할 때 사용할 수 있다. 또한 고정점 방법은 뉴턴 방법(Newton’s method) 등의 수치해석 알고리즘의 기반이 되기도 한다.

공학 등에서는 반복법을 사용하여 최적해를 찾는 경우가 있는데, 이때 반복법의 수렴성을 증명하는 데 사용되기도 한다. 강화학습에서 value iteration의 경우, 각 시행 단계가 축소사상임을 보임으로써 해당 방법의 수렴성이 보장된다.

참고문헌

• https://en.wikipedia.org/wiki/Banach_fixed-point_theorem
• https://en.wikipedia.org/wiki/Fixed-point_iteration
• Walter Rudin, Principles of Mathmatical Analysis (3rd Edition, 1976)